在实际工作中,AB实验是一种常用的验证方法,但还是有不少同学立即比较困难。这篇文章,作者通过一个生动的案例,为我们详细说明AB实验具体是个啥。

AB实验由于以统计学为基础,并且在实际应用过程中,又产生了一些新的方法论,存在较多专业术语,理解和使用门槛较高。
另外还存在一个普遍的现象,平时沟通时不时提及一些实验术语,但是却没有真正理解其原理,导致一旦出现问题,脑袋就像被猫抓乱的毛线球,完全不知道从哪里下手。一顿术语猛如虎,结果基础都没懂,喵~
二、这篇文章的目的本文的目的在于厘清互联网 AB 实验的核心思路。通过剖析互联网 AB 实验的原理,以及在实际应用中的方法,让读者能够清楚地了解其背后的逻辑。读完后,能知道那些常见的专业术语为什么被提出(在实际应用中,为什么被提出,比是什么更重要)。当出现问题,能够有更清晰的全局思维来定位。
老规矩,文中所提及的术语会标蓝,可自行扩展阅读。
三、互联网AB实验的核心思路笔者认为,互联网AB实验的核心思路是:利用数据去证明“设想”是否“靠谱”。
里面有两个关键词“设想”和“靠谱”,为了方便大家更易理解,抛几个自问自答:
1、为什么要有“设想”这一步?不可以直接从数据表现里推导出结论吗?目前来说,是不可以的。因为互联网AB实验的数学基础,就是建立在假设验证之上。我们需要先有一个“设想”,即某个变量可能对整体有或者没有影响,然后通过实验数据来验证这个设想是否成立。当然,可能没准儿哪天有新的数学突破能绕过假设呢?但在此之前,我们仍然需要依靠假设验证来进行AB实验,否则会存在事后解释的问题。
2、为什么是“靠谱”,不是“正确”?这是因为,在统计学中,任何实验结果都有犯错的概率。第一类错误是“弃真”,即拒绝了正确的假设;第二类错误是“纳伪”,即接受了错误的假设。在样本一定的情况下,无法同时降低第一类和第二类错误的概率。因此,我们需要在两者之间做出权衡。通常,我们会尽量不犯第一类错误,这是因为“弃真”后,我们可能会真正错过一个有效的策略,而“纳伪”后,我们还可以有其他机会发现它是错误的。
3、那怎么衡量有多“靠谱”呢?以及多靠谱才算“靠谱”?前面说到尽量不犯“弃真”错误。我们常见的“P值”可以姑且被看作是犯“弃真”错误的实际概率(衡量具体有多靠谱),而“显著水平α”就是犯“弃真”错误的概率上限(我们自行设定的靠谱标准), P值像我们考试的得分,α像我们考试的合格线。所以按照这个思路,我们的设想会有一个“成绩”P值,然后和α比较下,看这个设想有没有“合格”。
另外我们的设想往往是估一个区间,比如假设某指标提升x%以上(正向,单尾检验)或者减少x%以上(负向,单尾检验)或者指标有变化(双尾检验)。区间估计的范围越大,包含真实参数值的概率就越高,但精确度会相应降低。这就像我们小时候让父母猜考试成绩,父母说‘60分以上’(一个较宽的区间估计)比说‘90分以上’(一个较窄的区间估计)更有可能猜中,但如果我们实际考了91分,那么后者的精确度会更高。同理,‘有提升’肯定比‘提升x%以上’更容易猜中(拿到“合格证”),但是精确度没那么高,对业务的指导价值会更有限。
那可以“合格”的同时又尽量“精确”吗?按前面的思路,如果富有经验可以,否则不太行。于是我们换了一种思路,不看P值了,只看合格线。拿合格线(置信水平1-α)来倒推这个指标的区间在哪里(置信区间)。
所以总得来说,如果你有一个明确的指标预期,可以直接使用P值来判断;如果你没有很明确或者希望探索更广泛的可能性,使用置信区间更为合适,目前后者在业内使用更广泛。
四、互联网AB实验的难点及各类方法在实际工作中,当我们要利用数据去证明“设想”的时候,不外乎是把“设想”作为一个变量,注入到流量里,然后看这个流量有没有变化。方法论有,思路也简单,那难在哪里呢?
互联网AB实验是以统计方法论为基础(数学层),将其尽可能转化应用到实际的业务中(操作层)。对于我们来说,真正的难点并不在数学层,而是在转化应用的过程中,要同时满足业务需求和数学条件,而采用的各类方法以及数据解释。
可能有些抽象,为了方便理解,笔者将业务需求和数学条件进行了归类
3类业务需求:用户体验、流量切分、数据解释
3个数学条件:单一变量原则、样本随机且足量原则、显著性原则
注:互联网AB实验主要是以“样本A和B在部分指标上是否存在显著差异”(独立样本T检验/双样本Z检验)的方式进行实验,因此本文的数学条件基于该方式提出。
下面我们围绕3类业务需求,来阐释在操作层可能遇到的问题,以及业界对应的各类方法。
1、用户体验实验本身的目标是向用户推出一系列被证实过的“好设想”从而提升用户行为。但在实验执行的过程中,可能会存在与用户体验相悖的情况,因此平台需要在实验设计时充分考虑用户体验的问题。比如:
实验是为了验证“设想”,在拿到实验结果前,我们没法确定这个设想是好是坏。如果是坏的设想,对用户体验自然会有负影响,同时坏的实验往往会被停止,用户前后的体验会不一致。基于此,实验的范围越小越好。但是在数学条件里又要求“样本足量原则”,因此在实验前往往需要做最小样本量评估。
另外,互联网里的一个“用户”,可能是一个设备/账号ID、或者请求ID,如果某个实验的改动在用户体验上有所感知(比如UI调整),那为了用户体验的一致性,则需要使用设备/账号ID来作为“用户”,保证至少在实验期间,同一设备/账号所感知到的体验是一致的。
2、流量切分数学条件里的单一变量原则、样本随机且足量原则都需要在流量切分里进行体现。而实际业务中,会存在一些限制,包括:
(1)流量不够
从业务视角来说,往往希望能同时进行多个实验(1个月做100个实验和1年做100个实验,对于业务的价值可能是不同的,竞争越大的业务,时间越值钱)。
但同一时间段下的流量是既定的,而数学条件又要求足量原则。因此,为了在同一时间下产生更多可用的实验流量,即提高流量使用效率,业内有两种常见方法:
a、省着用。一个实验需要的流量按最小样本量评估。就像用水一样,假设你今天有5件家务要做,家里只有10盆水,在“省着用”的思路下,你按每件家务的最小用量进行评估,然后将这5件家务的用水量进行汇总,只要不超过10盆水那“省着用”就足够了~在这里,每滴水只会被1件家务所使用,这是实验里的流量互斥概念。
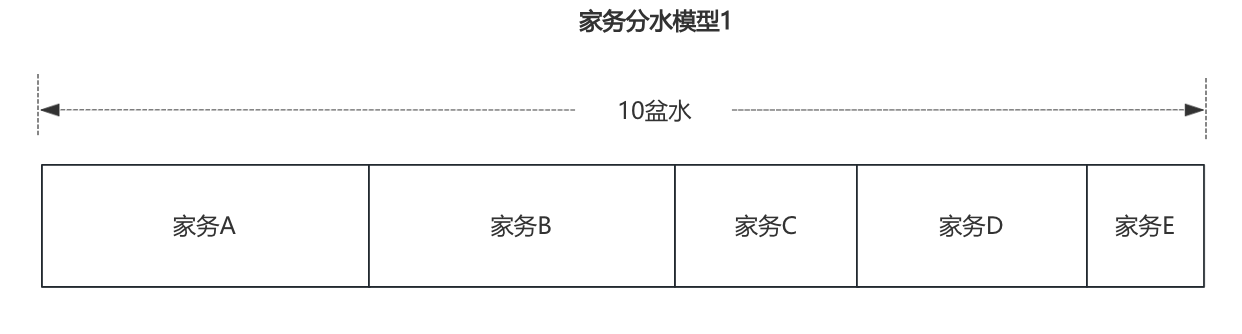
b、重复用。当然,每滴水也可以被多件家务使用,这是节约用水的常见思路,也可以对应实验里的流量正交概念。
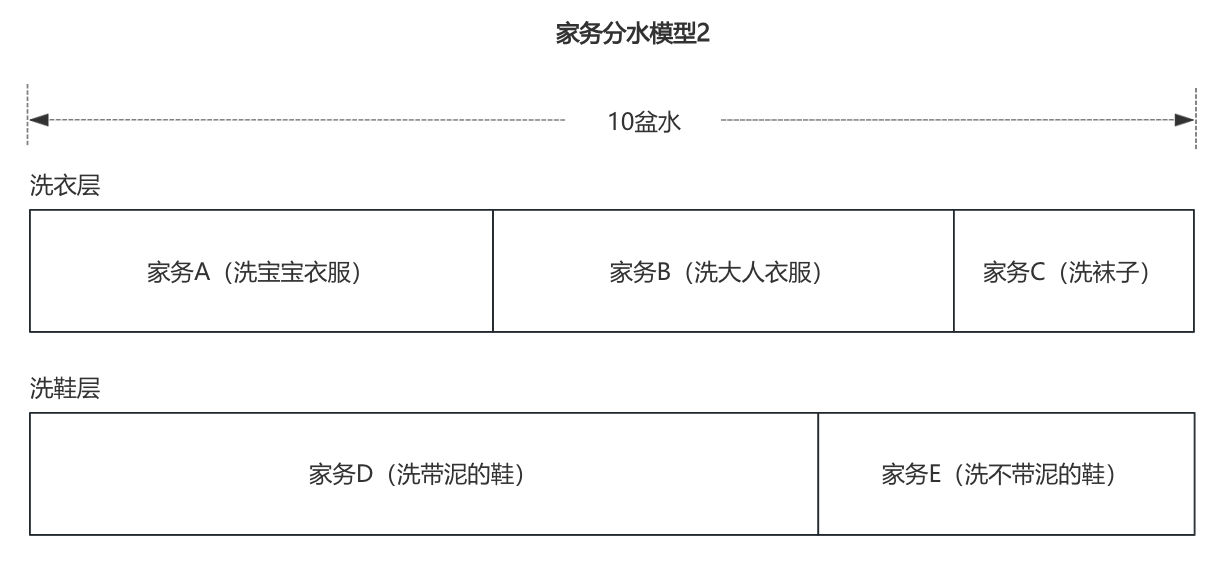
假设5件家务里,有3件家务(洗宝宝衣服、洗大人衣服、洗袜子)属于洗衣类的,2件家务(洗带泥的鞋、洗不带泥的鞋)属于洗鞋类的。那你可以把水先全部用在洗衣类家务,洗完后,把这10盆水混合到一起,再进入下一层的洗鞋类家务。
这里水被使用在了两层,第一层洗衣层、第二层洗鞋层,每一层都有10盆水可用。
另外你突然想起昨晚的碗还没洗。由于洗碗水无法和其他家务重复使用,因此做家务的水整体需要被划分成两个区块,第一个区块专门洗碗(4盆水),第二个区块给其余家务(剩6盆水)。但是你发现第二区块的6盆水不够洗衣类的最小用水,富有家务经验的你把洗衣层再分成了洗衣服层和洗袜子层。
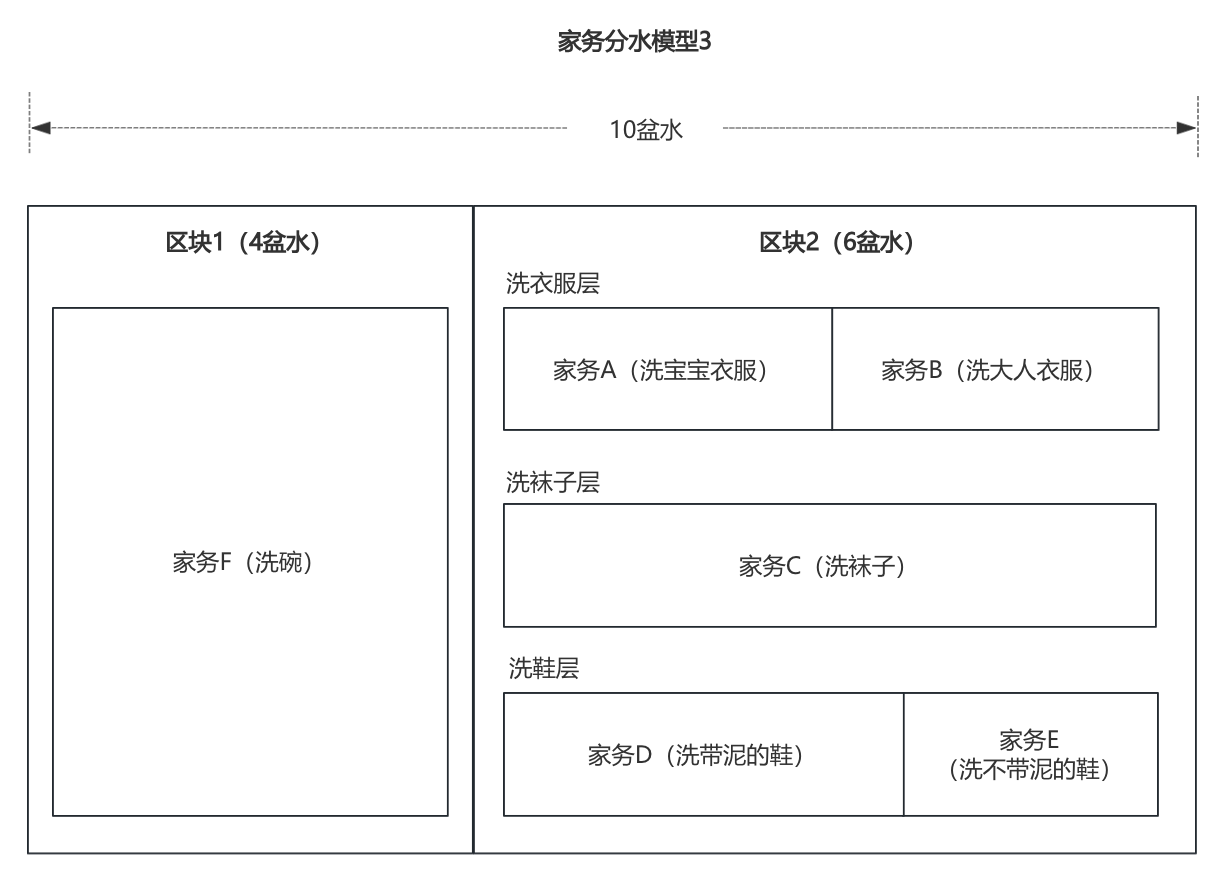
上面的分水模型是不是和实验分流模型高度相似?针对“流量不够”这一业务限制,业内采用的方法思路其实和咱们“节约用水”的思路差不多,只是实验分流没有层级先后顺序,流量可以从任一层灌入。
(2)流量差异
实验流量与“大盘”流量两者存在差异,这个不难理解,但可能很多读者没有理解到差异具体在哪,这点对于后文的数据解释很重要,我们来捋一捋~
实验是通过切小部分流量来证明设想,证明OK后将小部分流量切到全量。如下图,业务所希望减少的差异实际上是“实验”与“放量后的大盘”之间的差异。这个差异可以拆分为“实验”与“实验所在大盘“的差异、“实验所在大盘”与“放量后的大盘”的差异。
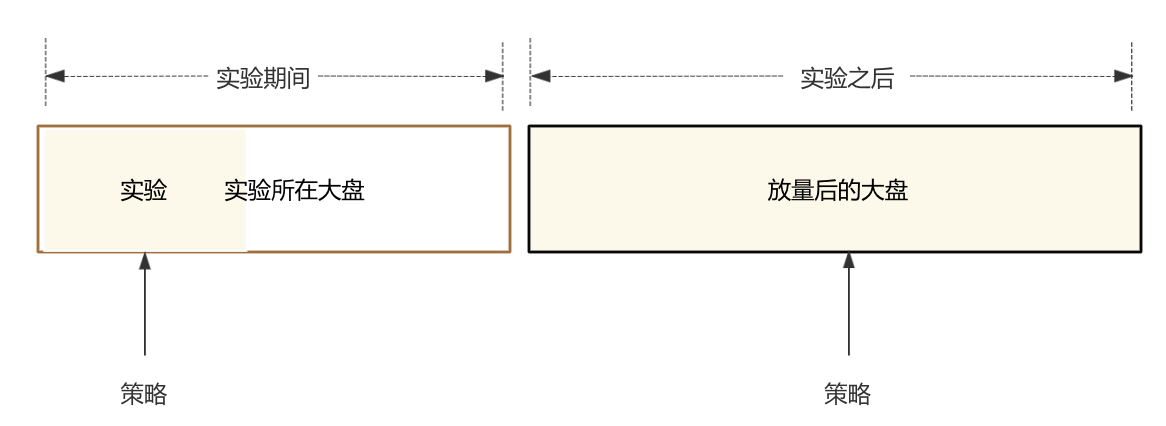
a、“实验”与“实验所在大盘“的差异
要想减少这部分的差异,就是尽可能均匀且随机得筛出一批“用户”,能让这些“用户”代表总体。常见的筛选方法是哈希计算。
另外,为了以防筛选方法没用对、或者方法不适用,可以在实验之前,提前进行流量切分,不加策略观测所切分的流量是否能代表“大盘”(空跑期AA实验)。
b、“实验所在大盘”与“放量后的大盘”的差异
这里的差异在时间,而时间所引入的变量我们并不可控。因此相比前面的差异,这个差异我们显得束手无策。减少它的方法很少,更多是解释它。后文会展开如何解释。
(3)人为犯错
上面两点“流量不够”“流量差异”的限制都是客观存在的,更多依赖技术手段解决。但由于流量切分有一定的专业门槛,还可能受“人为犯错”所带来的限制,举两个比较常见的例子:
a、实验切流对象混淆
要搞清楚实验切流的对象是谁,前提是先确定好实验的设想是什么。
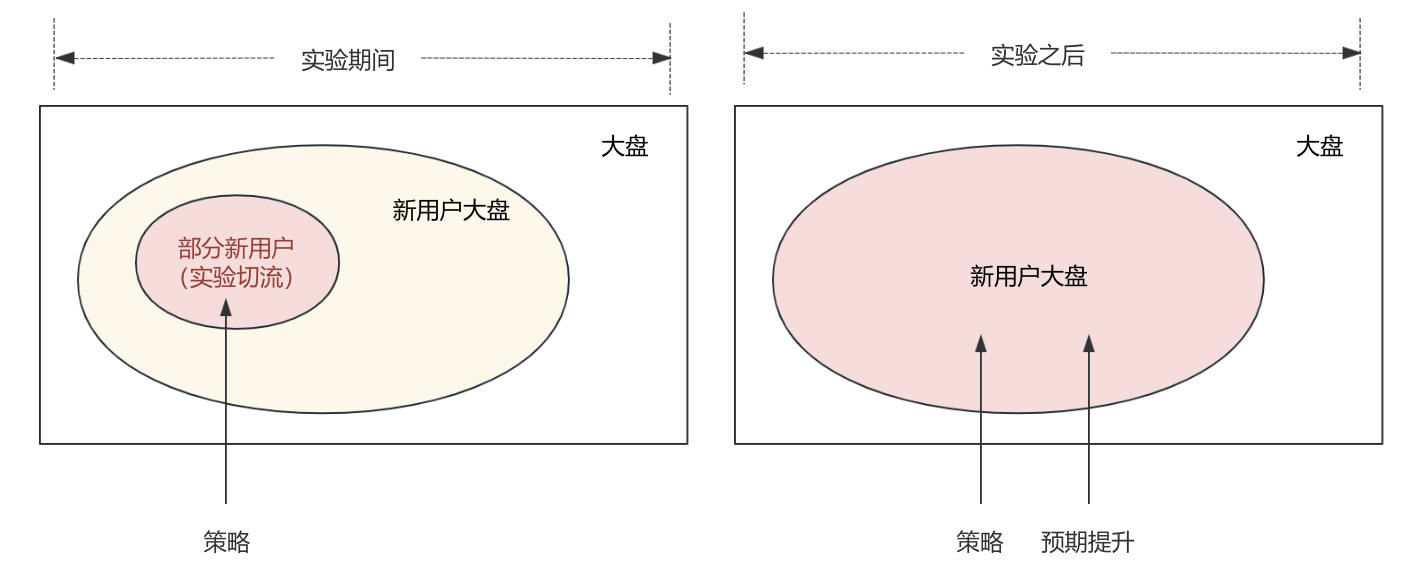
假设你有个设想1:“在首页给新用户推荐热门内容能提升新用户的次日留存率”。
在这个设想下,策略是针对新用户,观测的指标也是新用户。所以实验切流对象是“部分新用户”,实验OK后放量所预期提升的是“新用户大盘”指标。如下图
然后你又有个设想2:“在首页给新用户推荐热门内容能提升整体用户的次日留存率”。
设想2相比1,策略不变,但是观测的指标不再是新用户范围,而是大盘用户。所以实验切流的对象是“部分大盘用户”,实验OK后放量所预期提升的是“大盘用户”指标。如下图
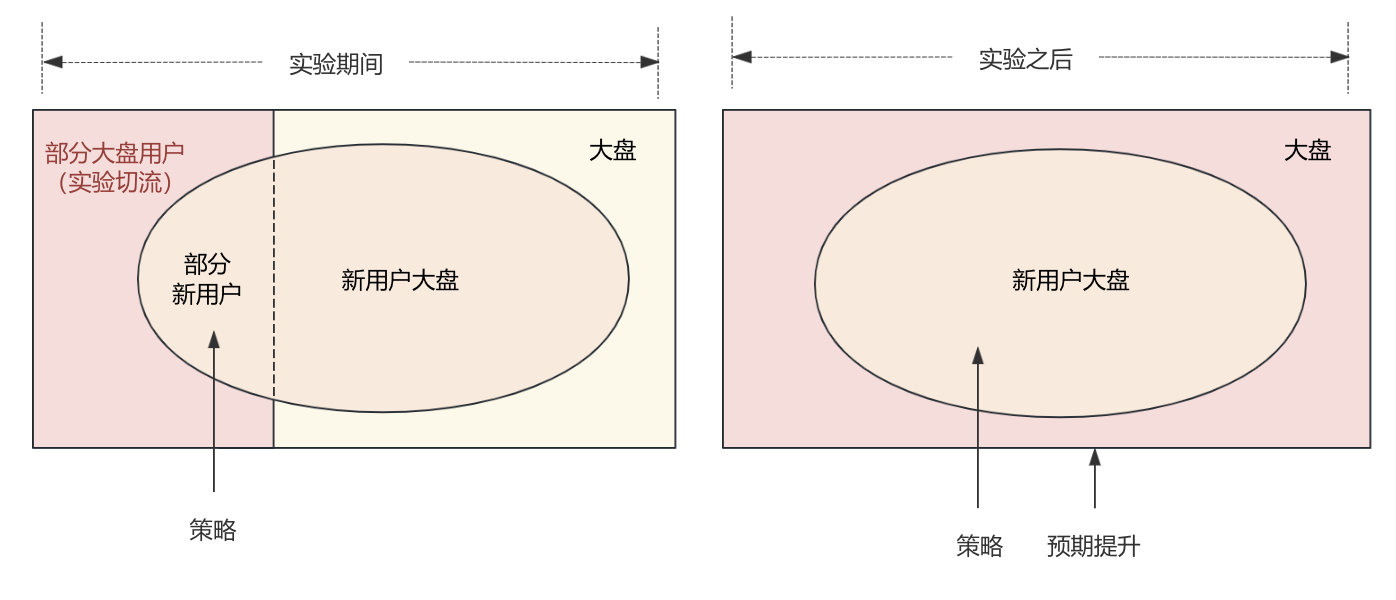
设想1和2由于观测的指标范围不同,所以切流对象也不同。在实际工作中,会出现切流对象混淆的情况,如果设想1用了设想2的切流方式,即观测的是新用户,但是用大盘切流(即包括了新用户和老用户在内的所有用户),那会导致指标结果被稀释,影响实验结果的准确性;而如果设想2用了设想1的切流方式,即观测的是大盘用户,但是用新用户切流,那其实根本无法得到指标结果。
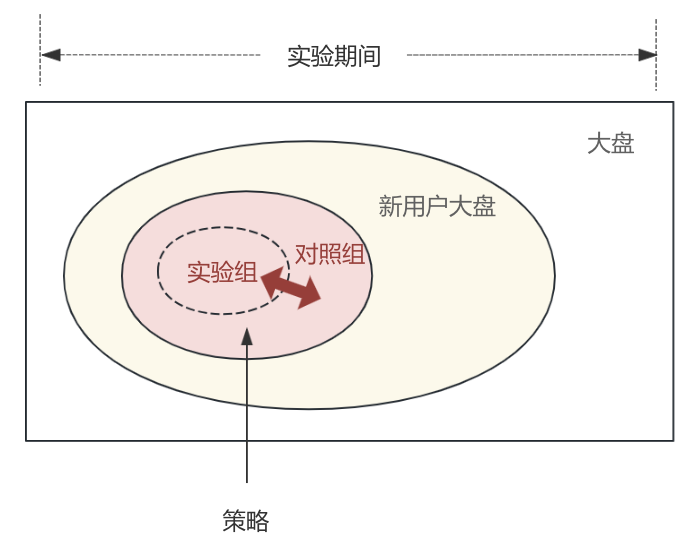
b、实验组与对照组互相影响
假设你又有个设想3:“在首页引导新用户发布内容能提升新用户的次日留存率”。即在策略上把“给新用户推荐热门内容”改成了“引导新用户发布内容”。
这里会有个问题是,实验组里用户发布的内容,会不会被对照组里的用户看到,如果会,那就存在实验组与对照组互相影响的问题,因此针对这种情况,需要评估并进行隔离。
实际工作中,如果没有提前考虑到实验组和对照组互相影响的问题,就可能导致实验结果不准以及很难解释。这在内容生产、社交功能上比较常见。
理想中的情况是,实验时相关指标都升了,然后放量,相关指标如预期获得提升,年终奖蹭蹭上涨。但现实情况却可能五花八门,所以我们需要对这些五花八门的情况进行数据解释,以利于后续策略的提出。举几个例子:
(1)实验期指标升了,但放量后指标没有提升或者甚至降了
如果排除切流问题(“实验流量”无法代表“实验所在大盘流量”),那原因就在前面所提到的“实验所在大盘”与“放量后的大盘”的差异上了。这个差异由时间所引入,如前所述,更多是解释它。
由于我们所统计的数据,都是来源于用户行为,所以时间所引入的变量最终都是表现在用户行为变化上。即,我们需要解释的问题实际是:不同时间下,用户可能会因为哪些影响而发生变化。
a、所处的平台影响
即平台的其他策略影响了用户。一种是平台的其他策略直接导致用户行为下跌;另一种是平台的其他策略影响了用户的分布,即用户占比变化导致的数据下跌(辛普森悖论)。
插个楼:“占比不均”所引入的一系列“反常识现象”是个很有趣的话题,在我们进行数据分析、甚至日常生活中会时常碰到,后面有时间笔者会单独写篇文章进行介绍~
b、所处的时长影响
在实验期,由于有时间限制,在这段时间里(比如2周)用户行为确实涨了,但是过了这个时间用户可能对新功能失去了新鲜感,行为数据开始下跌(新奇效应)。针对这种情况,可以通过拉长实验时间的方式在一定程度上规避这种问题;
c、所处的时间节点影响
实验期间可能正好遇到大促这类季节性节点,这类节点下可能会让切流之间本身就出现差异。针对这种情况,为了后续更好解释数据,可以再单独切一个对照组,即有2个对照组,看实验期间两个对照组之间的差异(实验期AA实验)。
需要说明的是,实验期AA实验这种方式能解释的数据仅限于“由于季节性节点所导致的分流不均”,无法解释“由于季节性节点所弱化或者强化的实验组和对照组之间的差异”,比如原本差异是5%,由于季节性节点差异10%。
(2)用不同的数学标准,实验结果不一致
前面提到的置信水平1-α设定的值不同,结果不一致。即实际考了70分,按照60分合格线算过关,但按照80分合格线就不行了。这个只能基于实际的业务情况来判断,如果对实验的风险容忍度低,那合格线就得设得高,反之亦然。
(3)X指标升了Y指标降了
这个也只能基于实际的业务情况来判断,并且为了让这种判断有更多的依据,所以需要在实验设计时就提前考虑核心指标、辅助指标、反向指标是什么。如果X只是辅助指标,核心指标并没有提升,那这个实验结果自然无法放量;如果X是核心指标,则需要衡量业务对Y的接受度。
(4)开放了多个实验,如何衡量这些实验一起对平台的价值
今年部门可能做了很多实验,有些策略让实验指标正向显著,但这些策略加在一起整体对部门的核心指标提升多少呢?为了解答这个问题,部门会通过预留一部分不加任何策略的“干净”流量来进行观测(holdout桶,常见于推荐系统)。
五、最后强调几点:
1、如果不是在这块有非常扎实的基础,请不要使用非业内常规的分流方法。否则会加大数据解释的难度(甚至可能根本无法解释)。
2、试错也有价值,客观解读,接受实验的失败,这才是实验的意义。
3、笔者能力有限,外加为了让文章尽可能通俗,在阐述上有较多不严谨或不全面的地方。欢迎大家指正探讨。